規則性を見つけるスクラッチ×マインクラフト 5回目

前回はドアのblockData値を少し詳しく見ていきました。
ドアは少し特殊なようでうまく組み合わせないと思ったように設置できないことがわかりました。
それでは豆腐ハウスの屋根を改良するプログラム例から
すでに屋根がある場合はblockTypeId0で上書きするか壊してからやるといいかもしれません。

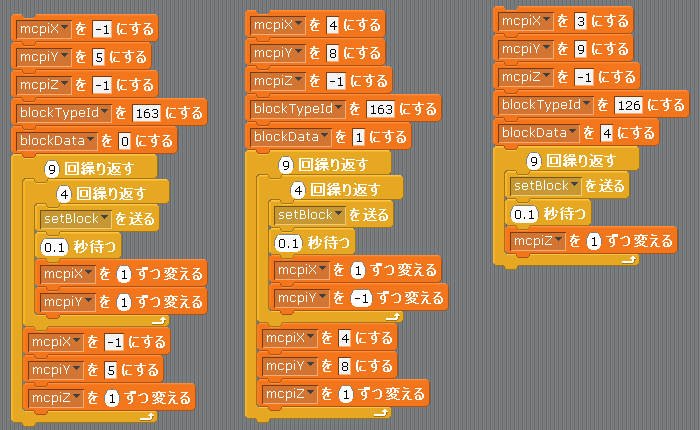
あくまでプログラムの例です。
豆腐ハウスの壁から組み合わせていくとレンガの壁にアカシアの屋根というなんだか妙な組み合わせになっています。
ハシゴも意味がなくなりますし・・・
いっそのことすべてアカシアで設置したほうがいいかもしれませんね。
それにしても結構なブロック数になりますね。
大きな建造物を作ろうと思ったらかなりの量になることが容易に想像できます。
しかもプログラム例で作成してきたプログラムはすべてX、Z座標に対して平行に、四角になるように設置してきました。
Y座標は屋根の設置のところで斜めに設置しましたがそれにしても階段状の設置だったので面倒ではありませんでした。
ではX、Z座標に対して斜めに敷き詰めて設置してみましょう。
完成例は以下の画像です。

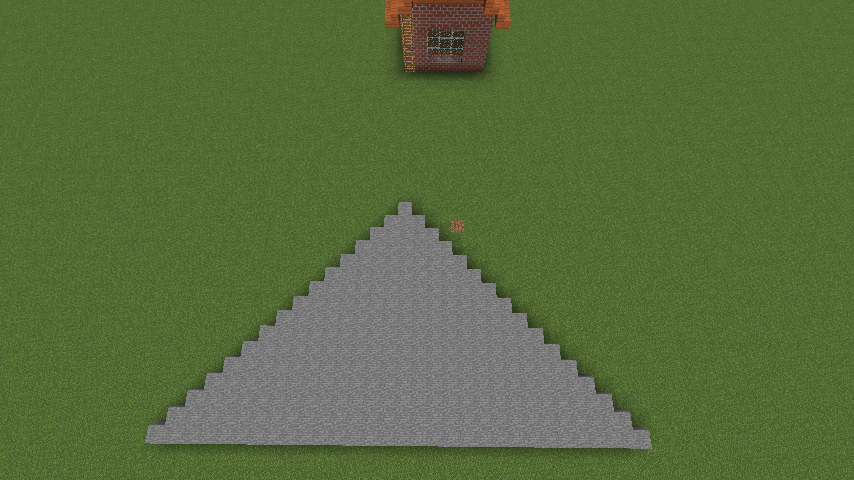
三角形型に設置する感じですね。一番上の1個を設置して次に2番目の3個を設置、次に3番目の5個を設置というようにして16番目まで設置しています。
以下にサンプルプログラムを載せますがあくまでも一例ということを理解してください。

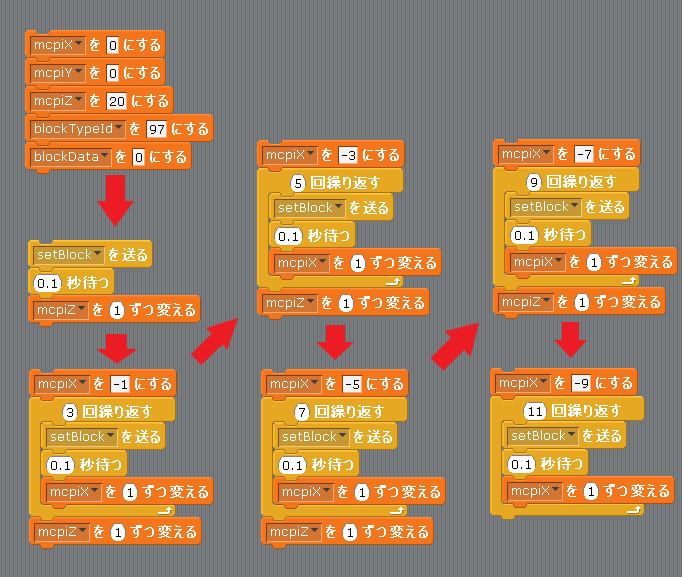
プログラムの実行順は矢印順です。
このようにまずは座標やblockTypeId、blockDataを指定してそれから1段ずつ地道に設置していくプログラムを作り順番に実行していく方法です。ここでは6段目までのプログラムとなっています。
1段目に1つ設置してZ座標を移動して、2段目のスタート地点の座標を指定して再度設置していき同じような方法を続けて6段目まで設置しています。
非常に面倒です。

少し話を変えましょう。
なぜプログラムを組むのか？
という質問があったとします。
答えはたくさんあるでしょう。
人が楽をするため、だとか
決まった動作を繰り返し行わせるため、だとか
面倒な計算をさせるため等があると思います。

カンのいい方は気がついているでしょう。話を戻します。
今回のオブジェクトの敷き詰めですが設置が斜めになったことで繰り返すを2回セット(縦×横)にして楽に設置する方法が使えないので一列ずつ設置したプログラム例になっています。
左右のどちらからか数を増やしながら設置を始めて、真ん中まで来たらプログラムを切り変えて減らしながら設置する方法をとれば多少は楽です。
だが、しかしこの斜めに設置するプログラムを実は簡潔にまとめられます。
1段ずつ地道に設置する先ほどの例を再度見てみましょう。

ある程度の法則があることに気が付けば道は見えるかもしれません。
ポイントは規則的に変わっていく数値です。

まず簡単なところから見ると設置するプログラム自体は今までと変わらず繰り返しの命令です。そしてmcpiZは1段設置するたびに1増えています。これも今まで通りです。
あと残っているのはmcpiXの指定と設置の回数です。
ではmcpiXはどのように指定しているのか？
最初は0、次は-1、次は-3、次は-5、次は-7、次は-9です。
では個数を見てみましょう。
最初は1個、次は3個、次は5個、次は7個、次は9個、次は11個です。
個数のほうが法則は簡単ですね、2段目以降は1段ごとに同じ数が増加しています。
これは決まった動作です。縦書きにすると
1段目は1個
2段目は3個
3段目は5個
4段目は7個
5段目は9個
6段目は11個
こうなります。
同様にmcpiXも並べてみましょう。
1段目は0
2段目は-1
3段目は-3
4段目は-5
5段目は-7
6段目は-9
最終的にはこれで16段目まで設置します。
一見規則性があるように見えますが、わかりますか？
ちょっと難しいですよね。

ではまたプログラムの話を少ししましょう。
わからなくなったら別のことを考えてリフレッシュしましょう。
プログラムをはじめいわゆるデジタルデータというものは0と1で記憶されています。
2進法というものです。
普段日常生活で使用しているのは10進法です。ほかには60進法も考えればわかるかもしれません。
ドアの回でも少し触れましたがオフとオンにも該当します。
パソコンの電源ボタンや壁のスイッチ、パソコン、スマホの設定画面のアイコンなどにも0と1はデザインとして使われています。
10進法：2進法で表すと
0は0
1は1
ですが
2は10
3は11
4は100
5は101
という感じです。
ともに0から始まるのは同じですね。
マインクラフトの各座標も0から始まっています。

さて話を戻してまずはわかっているほうからプログラムを組んでみましょう。
4段くらいまでオブジェを設置してみましょう。
X座標のプログラムはとりあえず置いておきましょう。
連続して設置していくとX座標は1ずつ増えるので
設置イメージは下記の図のような感じです。

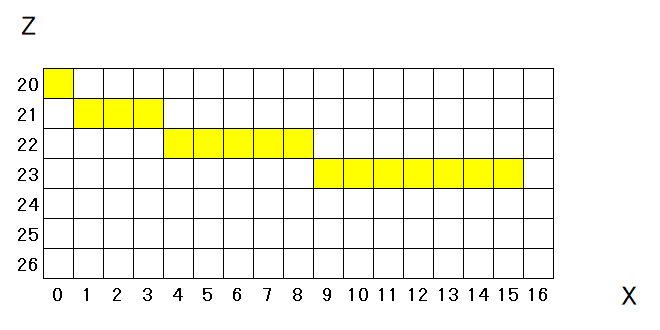
1段目1個
2段目3個
3段目5個
4段目7個と設置するわけですね。
設置したらX座標が1増加するプログラムになっているので次の段の設置開始座標は一つ右にずれています。
考え方はいろいろありますが1段上の数より2個ずつ増えているので+2を分けて考えると
1…1
2…1+2=3
3…3+2=5
4…5+2=7
とすることもできます。
段数、段数+2、(段数+1)+2、((段数+1)+1)+2+2
というような感じです。

そこでもっと簡単な方法はないか考えてみます。
段数と個数の関係をよく見ると段数×2-1となっているのがわかります。
1×2-1=1
2×2-1=3
3×2-1=5
4×2-1=7
と言うことでどうにか段数(回数)を設定、もしくは取得できれば設置ができそうだということがわかります。
どのように取得するかというと座標と同じです。
座標はどのように取得しているのか？
変数ですね。
では段数の変数は何か？
ありません！
だから自分で作るのです。
変数を自分で設定して使えるようになると一気にできることが増えますし、プログラムも楽になります。
と言うことでそれはまた次回。